Friday, July 16, 2021
(COVID-19) கொரோனா குறித்த வதந்திகள்
1. உடல் முழுவதும் ஆல்கஹால் அல்லது குளோரின் தெளித்தால் வைரஸ் கிருமி சாகும் என்பது.
2. பூண்டு சாப்பிட்டால் கொரோனா தொற்று நோய் குணமாகும்
3. குளிர் மற்றும் பனி கொரோனா வைரஸை கொள்ளும்
4. வெண்ணீரில் குளித்தால் கொரோனா நோய் போகும்
5. கொசு மூலம் கொரோனோ தொற்றுநோய் பரவும்
6. வீட்டு பிராணிகள் மூலம் கொரோன் வைரஸ் பரவும்
7. ஹேண்ட் டிரையர் (கை உலர்த்தி) பயன்படுத்தினால் கொரோனை வைரஸை கொள்ள முடியும்
8. கொரோனா வைரஸ் முதியவர்களை மட்டும் தாக்கும்
Friday, July 2, 2021
கொழும்பு துறைமுக நகரம் Port City Colombo International Financial City, CIFC
துறைமுக நகரம் Port City என அழைக்கப்படும் கொழும்பு சர்வதேச நிதி நகரம் என்பது
2021 மே 20 அன்று இலங்கை நாடாளுமன்றம் கொழும்பு துறைமுக நகர் ஆணைக்குழு நிறுவுவதற்கான சட்டமூலத்தை 2021 மே 20 அன்று 91 மேலதிக வாக்குகளால் நிறைவேற்றியது
இலங்கையின் தலைநகர் கொழும்பில் அமைந்துள்ள
ஒரு சிறப்புப் பொருளாதார வலயமும், பன்னாட்டு நிதி மையமும் ஆகும். இக்கரையோர நகரம் காலிமுகத் திடலிற்கு அண்மையாக நிர்மாணிக்கப்பட்டு வருகிறது. இதற்கான நில மீட்புப் பணிகள் 2018 சனவரி 2018 யில் நிறைவடைந்தன. முழுத் திட்டத்திற்குமான செலவு 15 பில்லியன் அமெரிக்க டொலராக 2017 ஆம் ஆண்டில் நிர்ணயிக்கப்பட்டது.[1]இத்திட்டம் சீனாவின் பட்டை ஒன்று பாதை ஒன்று என்ற முயற்சியின் ஒரு பகுதியாகும்.[2] இந்நகரம் கொழும்பு துறைமுக விரிவாக்க செயற்றிட்டதின் கட்டுமான வளங்களை பயன்படுத்தி மேற்கொள்ளப்படும்.
DREDGING VESSELS
சீனா லேண்ட் கிராப் - உலகத்தை மறுவடிவமைக்க சீனா பயன்படுத்தும் மாபெரும் மணல்-உறிஞ்சும் கப்பல்கள்
WAN QING SHA
IMO: 9285768
MMSI: 412053050
Call Sign: BSPN
Flag: China [CN]
AIS Vessel Type: Other
Gross Tonnage: 10980
Deadweight: 12357 t
Length Overall x Breadth Extreme: 132.48m × 24.5m
Year Built: 2004
பாரிய கப்பல்கள்,மனதைக் கவரும் மணல், மற்றும் தென்சீனக் கடலில் விரிவாக்கத்திற்கான ஒரு பசி: மற்றவர்களைப் போல நில அபகரிப்புக்கான செய்முறை. இலங்கையின் வரலாற்றில் மிகப்பெரிய வெளிநாட்டு முதலீடான பாரிய சீன உள்கட்டமைப்பு திட்டத்தின் ஒரு பகுதியாக கொழும்பு கடற்கரையில் ஒரு புதிய நகரத்தை உருவாக்க வான் குயிங் ஷா உதவுகிறது. மிசிசிப்பி, பிலோக்ஸிக்கு தெற்கே உள்ள நீரில் பதினைந்து மைல் தொலைவில், மேகமற்ற வானத்திற்கு கீழே, சாம்பல்-கருப்பு குழம்பு ஒரு நுரைக்கும் நீரோடை ஒரு கப்பலில் நுழைகிறது. ஒவ்வொரு மூன்று விநாடிகளிலும், மெக்ஸிகோ வளைகுடாவின் அடிவாரத்தில் இருந்து வெளியேற்றப்படும் மற்றொரு டிரக் லோடு மதிப்புள்ள உப்பு நீர் மற்றும் மணல், எல்லிஸ் தீவின் பரந்த, திறந்த சரக்குப் பிடிப்பில் ஒரு ஹாப்பர் என அழைக்கப்படுகிறது. இந்த கப்பல் மிகப்பெரியது - இது அமெரிக்காவில் கட்டப்பட்ட மிகப்பெரிய அகழி. அதன் முன்னேற்றம், வடிவமைப்பால், மெதுவாக உள்ளது. இது ஒரு ஜோடி 30-டன் இழுவை தலைகளை இழுத்துச் செல்கிறது, இது எஃகு பற்களால் பதிக்கப்பட்டுள்ளது, இது மணல் கடல் அடிவாரத்தில் துடைக்கிறது. இரட்டை குழாய்கள், ஒவ்வொன்றும் மூன்று அடி (90 சென்டிமீட்டர்) விட்டம் கொண்டவை, இழுவைத் தலைகளை கப்பலின் டெக்கில் உள்ள பெரிய பம்புகளுடன் இணைக்கின்றன. பம்புகள் குழம்புக்குள் குழம்பை உறிஞ்சும், இது மெதுவாக ரோலிங் சாம்பல் சூப்பால் நிரப்பப்படுகிறது, சளி, சாப்ட்பால் அளவு குமிழ்கள் கொண்டது.
JUN YANG 1
IMO: 9714472
MMSI: 413487270
Call Sign: BSPS
Flag: China [CN]
AIS Vessel Type: Unspecified
Gross Tonnage: 20406
Deadweight: 33030 t
Length Overall x Breadth Extreme: 170.2m × 30m
Year Built: 2016
Friday, December 4, 2020
What is a Beam? and Types of Beams பீம் என்றால் என்ன? பீம்ஸ் வகைகள் என்ன?
What is a Beam?
Beam Definition: What is a Beam?
A beam, in Structural Engineering terms, is a member that can be comprised of a number of materials (including steel, wood aluminum) to withstand loads – typically applied laterally to the beam axis. Beams can also be referred to members, elements, rafters, shafts or purling.
A beam can exist within a frame, a truss or on its own as its own structure. SkyCiv also has some write ups of each of the different types of beams, including cantilever beam, or continuous beam.
Beam Shapes
Beams can come in a wide range of shapes that have different applications and strength purposes. Some common shapes are i beams (as shown in the 3D renderer above), T-beams, channel sections, rectangular, hollow rectangular and pipes. Regardless of the shape, they are all considered beams. In analysis and design, they are often picked up from different manufacturer libraries and databases so that the industry is all modeling structures based on the same shapes and dimensions.
Types of Beams
Support Configuration
The most common way that structural engineers classify beams is by their support configuration, there are many possible configurations however, these are the 4 most common types:
- Simply Supported
- Cantilever
- Continuous
- Fixed-Fixed
Simply Supported Beam
 Source: SkyCiv Beam
Source: SkyCiv Beam
Simply supported beams are defined as having two supports at either end – one pinned and one roller. This is generally considered as being the most simple type of beam. This is a very common type of beam and is determinate because there are three equilibrium equations and only 3 unknown reactions. 2 from the pinned support and 1 from the roller support.
Cantilever Beam
 Source: Cantilever Beam Calculator
Source: Cantilever Beam Calculator
Cantilever Beams are supported from one end, using a Fixed Support. This is the only type of support that can be used in this scenario as it offers the moment resistance required for the beam to remain stable. If a pinned or roller support was used, it would not offer the moment restraint that the beam would need. A good example of a cantilever beam is a shop awning – where the beam is bolted directly into the wall. This is also a determinate beam because there are only 3 unknown reactions which, is equal to the number of equilibrium equations available.
Continuous Beam
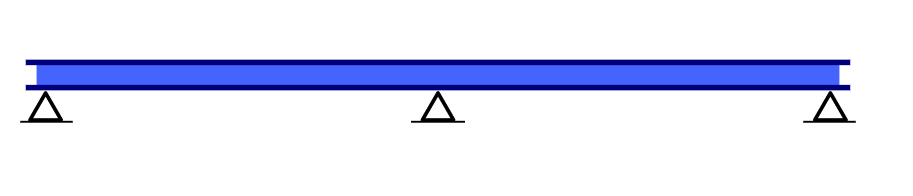 Source: SkyCiv Beam
Source: SkyCiv Beam
Continuous beams are multi-spanned beams that have multiple supports across the length of the beam. An example of a continuous beam would be a single beam that is supported by a number of columns along its length. This beam is indeterminate since there are more unknown reactions (6) than equilibrium equations available (3). This is then called a level 3 indeterminate beam.
Fixed Beam
 Source: SkyCiv Beam
Source: SkyCiv Beam
Fixed Beams have fixed supports at either end – offering moment resistance at either end. This type of beam may be used when the designer wants to control the deflection at the mid-span because the two fixed supports prevent rotation. This beam is also indeterminate as the unknown reactions (6) are greater than the equations available (3). This is also a level 3 indeterminate beam.
Overhanging Beam
 Source: SkyCiv Beam
Source: SkyCiv Beam
Overhanging beams are those with two supports, but unlike simply supported beams, one of the supports is not at the end of the member. A typical example of this is a balcony which is being extended from a frame structure. The frame offers the two supports, yet no support exists at the end of the member – allowing it to ‘overhang’ as the name suggests. This too is an indeterminate beam as the number of unknown reactions (4) is greater than equilibrium equations (3). This is a level 1 indeterminate beam.
Thursday, December 3, 2020
How Connection Was Made Between Column And Brick Wall
How Connection Was Made Between Column And Brick Wall
Basic Components Of A Building
Basic Components Of A Building
1- SUB-STRUCTURE
2- SUPERSTRUCTURE
1- FOUNDATION
2- PLINTH
4- WALLS
5- COLUMN
6- FLOORS
7- DOORS, WINDOWS, AND VENTILATION
8- STAIRS
9- ROOF
10- BUILDING FINISHES
Thursday, November 12, 2020
Modern Surveying
Modern Surveying
Basic control surveys
Geodetic surveys involve such extensive areas that allowance must be made for the Earth’s curvature. Baseline measurements for classical triangulation (the basic survey method that consists of accurately measuring a base line and computing other locations by angle measurement) are therefore reduced to sea-level length to start computations, and corrections are made for spherical excess in the angular determinations. Geodetic operations are classified into four “orders,” according to accuracy, the first-order surveys having the smallest permissible error. Primary triangulation is performed under rigid specifications to assure first-order accuracy.
Efforts are now under way to extend and tie together existing continental networks by satellite triangulation so as to facilitate the adjustment of all major geodetic surveys into a single world datum and determine the size and shape of the Earth spheroid with much greater accuracy than heretofore obtained. At the same time, current national networks will be strengthened, while the remaining amount of work to be done may be somewhat reduced. Satellite triangulation became operational in the United States in 1963 with observations by Rebound A-13, launched that year, and some prior work using the Echo 1 and Echo 2 passive reflecting satellites. The first satellite specifically designed for geodetic work, Pageos 1, was launched in 1966.
A first requirement for topographic mapping of a given area is an adequate pattern of horizontal and vertical control points, and an initial step is the assembly of all such existing information. This consists of descriptions of points for which positions (in terms of latitude and longitude) and elevations above mean sea level have been determined. They are occasionally located at some distance from the immediate project, in which case it is necessary to expand from the existing work. This is usually done on second- or third-order standards, depending upon the length of circuits involved.
The accuracy of survey measurements can be improved almost indefinitely but only at increased cost. Accordingly, control surveys are used; these consist of a comparatively few accurate measurements that cover the area of the project and from which short, less accurate measurements are made to the objects to be located. The simplest form of horizontal control is the traverse, which consists of a series of marked stations connected by measured courses and the measured angles between them. When such a series of distances and angles returns to its point of beginning or begins and ends at stations of superior (more accurate) control, it can be checked and the small errors of measurement adjusted for mathematical consistency. By assuming or measuring a direction of one of the courses and rectangular coordinates of one of the stations, the rectangular coordinates of all the stations can be computed.
Triangulation
A system of triangles usually affords superior horizontal control. All of the angles and at least one side (the base) of the triangulation system are measured. Though several arrangements can be used, one of the best is the quadrangle or a chain of quadrangles. Each quadrangle, with its four sides and two diagonals, provides eight angles that are measured. To be geometrically consistent, the angles must satisfy three so-called angle equations and one side equation. That is to say the three angles of each triangle, which add to 180°, must be of such sizes that computation through any set of adjacent triangles within the quadrangles will give the same values for any side. Ideally, the quadrangles should be parallelograms. If the system is connected with previously determined stations, the new system must fit the established measurements.
When the survey encompasses an area large enough for the Earth’s curvature to be a factor, an imaginary mathematical representation of the Earth must be employed as a reference surface. A level surface at mean sea level is considered to represent the Earth’s size and shape, and this is called the geoid. Because of gravity anomalies, the geoid is irregular; however, it is very nearly the surface generated by an ellipse rotating on its minor axis—i.e., an ellipsoid slightly flattened at the ends, or oblate. Such a figure is called a spheroid. Several have been computed by various authorities; the one usually used as a reference surface by English-speaking nations is (Alexander Ross) Clarke’s Spheroid of 1866. This oblate spheroid has a polar diameter about 27 miles (43 kilometres) less than its diameter at the Equator.
Because the directions of gravity converge toward the geoid, a length of the Earth’s surface measured above the geoid must be reduced to its sea-level equivalent—i.e., to that of the geoid. These lengths are assumed to be the distances, measured on the spheroid, between the extended lines of gravity down to the spheroid from the ends of the measured lengths on the actual surface of the Earth. The positions of the survey stations on the Earth’s surface are given in spherical coordinates.
Bench marks, or marked points on the Earth’s surface, connected by precise leveling constitute the vertical controls of surveying. The elevations of bench marks are given in terms of their heights above a selected level surface called a datum. In large-level surveys the usual datum is the geoid. The elevation taken as zero for the reference datum is the height of mean sea level determined by a series of observations at various points along the seashore taken continuously for a period of 19 years or more. Because mean sea level is not quite the same as the geoid, probably because of ocean currents, in adjusting the level grid for the United States and Canada all heights determined for mean sea level have been held at zero elevation.
Because the level surfaces, determined by leveling, are distorted slightly in the area toward the Earth’s poles (because of the reduction in centrifugal force and the increase in the force of gravity at higher latitudes), the distances between the surfaces and the geoid do not exactly represent the surfaces’ heights from the geoid. To correct these distortions, orthometric corrections must be applied to long lines of levels at high altitudes that have a north–south trend.
Trigonometric leveling often is necessary where accurate elevations are not available or when the elevations of inaccessible points must be determined. From two points of known position and elevation, the horizontal position of the unknown point is found by triangulation, and the vertical angles from the known points are measured. The differences in elevation from each of the known points to the unknown point can be computed trigonometrically.
The National Ocean Service in recent years has hoped to increase the density of horizontal control to the extent that no location in the United States will be farther than 50 miles (80 kilometres) from a primary point, and advances anticipated in analytic phototriangulation suggest that the envisioned density of control may soon suffice insofar as topographic mapping is concerned. Existing densities of control in Britain and much of western Europe are already adequate for mapping and cadastral surveys.
fire safety
Introduction to fire safety Most fires are preventable. Those responsible for workplaces and other buildings to which the public have access...
.jpeg)
-
பொதுப் போக்குவரத்து வரலாறு 1907 - கொழும்பிலிருந்து சிலாபம் வரையான முதலாவது பொதுப் போக்குவரத்து அறிமுகம் 1940- ஒவ்வொரு வழிகளுக்குமான கட்டண...
-
எது சிறந்த வாட்ஸ்அப்? Which one is a better app, YoWhatsApp, GBWhatsApp, FMWhatsApp or WhatsApp? ஆரம்பத்தில் நான் ஜிபி வாட்ஸ்அப்பை பரிந்த...
-
STRUCTURAL ANALYSIS vs STRUCTURAL DESIGN A structure is an assembly of materials which can carry applied loads (forces). If an eng...




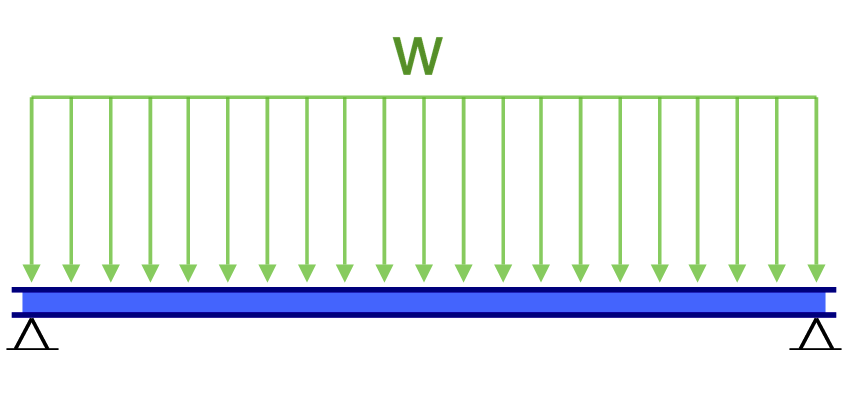 An example of a
An example of a 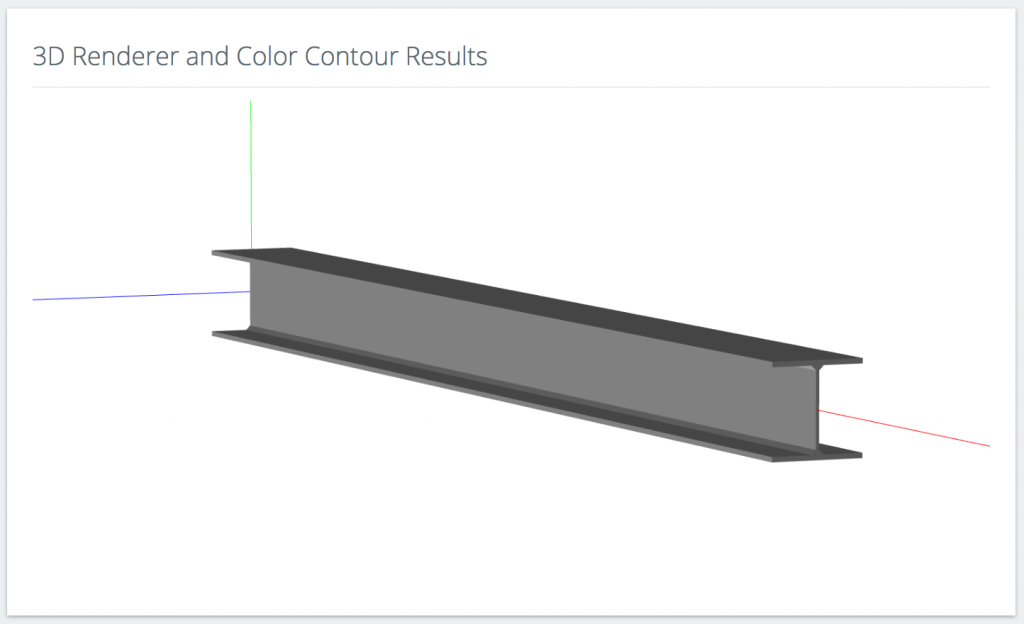 A 3D Rendering of an I-Beam
A 3D Rendering of an I-Beam



